
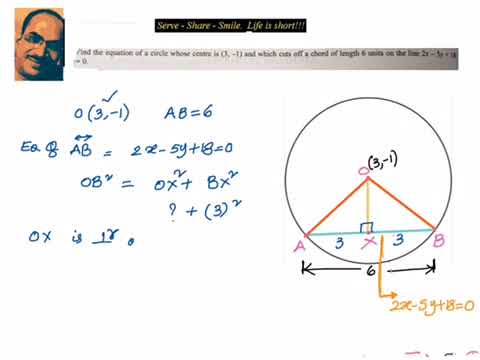
Therefore, the two basic formulas for finding the length of the chord of a circle are as follows We’ll you’re in the right place because that’s what this geometry lesson is all about. Thus using Pythagoras theorem, we may find the length of the chord CD easily. It is due to the fact that perpendicular drawn from centre O on chord CD will be the bisector of CD.

For example, the length of a chord can be used to find the circumference of a circle. We may also calculate the chord length if we know both the radius and the length of the right bisector. Chords can be used to solve problems in geometry. We may determine the length of the chord from the length of the radius and the angle made by the lines connecting the circle’s centre to the two ends of the chord CD. Calculate the distance between two chords. One chord has a length of t1 48 cm, and the second has a length of t2 20 cm, with the center lying between them.

the longest chord, ‘OE’ will be the radius of the circle and line CD represents a chord of the circle, whereas curve CD will be the arc. Two chords Two parallel chords are drawn in a circle with a radius r 26 cm. In the given circle having ‘O’ as the centre, AB represents the diameter of the circle i.e. The same two points are connected by the curve in the form of the corresponding arc in the circle. 3 Solved Examples for Chord Length Formula What is a Chord in a Circle?Ī chord is the line segment in a circle, which connects any two points on the circumference of the circle.


 0 kommentar(er)
0 kommentar(er)
